How To Graph The Solution Set

Solutions to Inequalities with Ii Variables

We know that a linear equation with two variables has infinitely many ordered pair solutions that form a line when graphed. A linear inequality with 2 variablesAn inequality relating linear expressions with two variables. The solution prepare is a region defining half of the plane. , on the other hand, has a solution set consisting of a region that defines half of the airplane.

Linear Equation	Linear Inequality
$y=\frac{3}{2}\mathrm{ten}+\mathrm{iii}$	$y\le \frac{\mathrm{iii}}{\mathrm{ii}}x+3$

For the inequality, the line defines the purlieus of the region that is shaded. This indicates that any ordered pair in the shaded region, including the boundary line, will satisfy the inequality. To see that this is the case, cull a few examination pointsA signal not on the boundary of the linear inequality used every bit a means to decide in which half-plane the solutions prevarication. and substitute them into the inequality.

Test point	$y\le \frac{3}{\mathrm{ii}}x+3$
(0, 0)	$\begin{array}{l}0\le \frac{3}{2}\left(0\right)+3\\ 0\le \mathrm{iii}\text{✓}\end{array}$
(2, 1)	$\begin{array}{l}1\le \frac{\mathrm{three}}{2}\left(2\right)+3\\ \mathrm{one}\le 3+3\\ 1\le \mathrm{half-dozen}\text{✓}\end{array}$
(−ii, −1)	$\begin{array}{l}-\mathrm{one}\le \frac{3}{\mathrm{two}}\left(-\mathrm{two}\right)+3\\ -\mathrm{ane}\le -3+3\\ -\mathrm{ane}\le 0\text{✓}\end{array}$

Also, we can see that ordered pairs outside the shaded region do not solve the linear inequality.

Examination point	$y\le \frac{3}{\mathrm{ii}}x+\mathrm{iii}$
(−2, 3)	$\begin{array}{l}3\le \frac{3}{2}\left(-2\right)+3\\ 3\le -3+3\\ 3\le 0\text{✗}\end{array}$

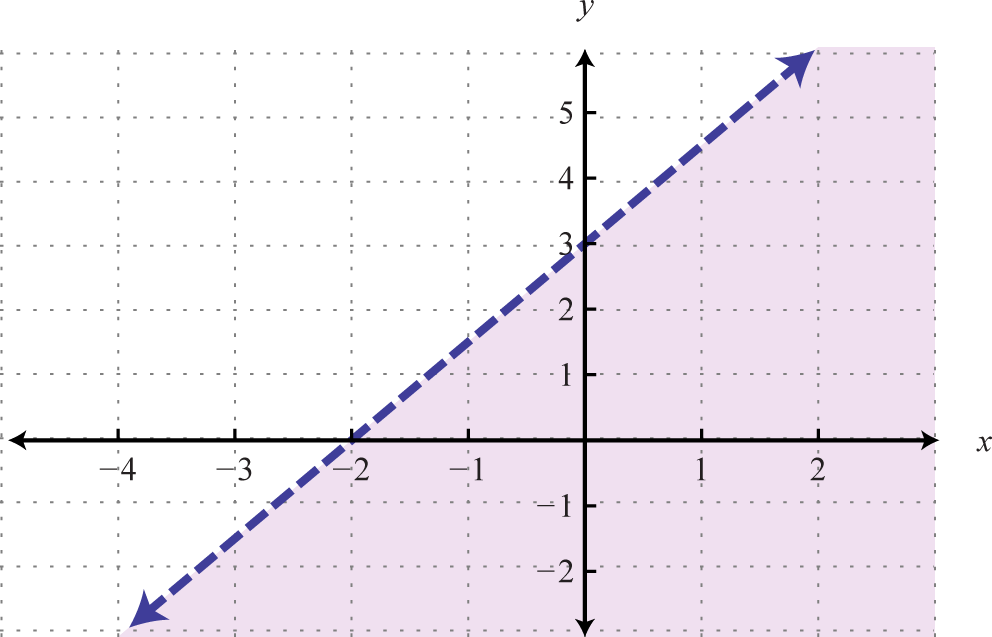
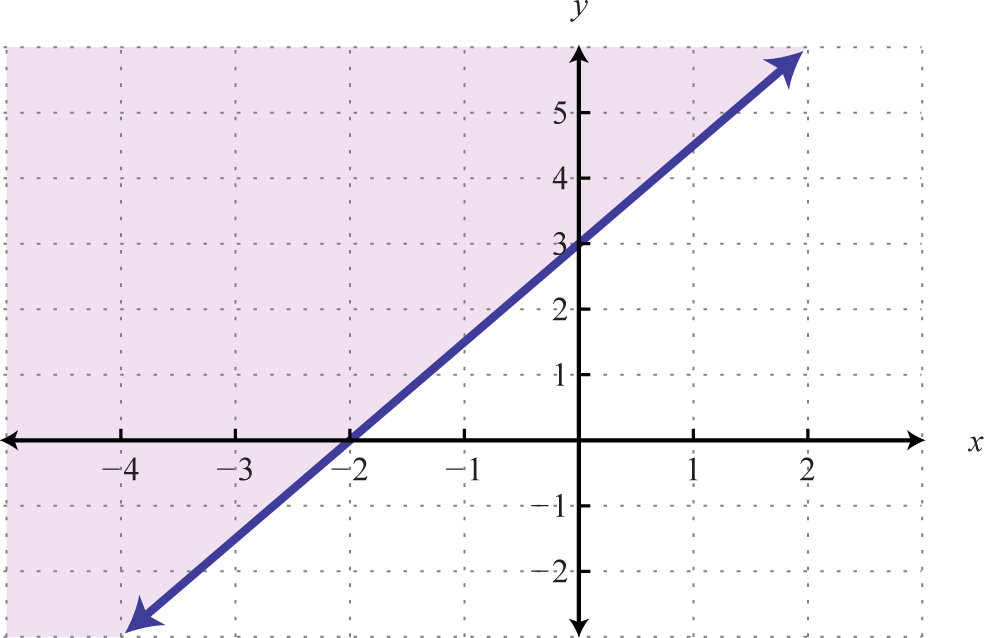
The graph of the solution set to a linear inequality is always a region. Nevertheless, the purlieus may not always be included in that prepare. In the previous case, the line was part of the solution gear up because of the "or equal to" function of the inclusive inequality $\le .$ If given a strict inequality $<$ , we would and then use a dashed line to indicate that those points are not included in the solution set.

Non-Inclusive Boundary	Inclusive Boundary
$y<\frac{3}{\mathrm{two}}x+3$	$y\le \frac{\mathrm{iii}}{2}x+\mathrm{three}$

Consider the point (0, 3) on the boundary; this ordered pair satisfies the linear equation. It is the "or equal to" part of the inclusive inequality that makes the ordered pair part of the solution fix.

$y<\frac{3}{\mathrm{two}}x+3$	$y\le \frac{\mathrm{three}}{2}x+3$
$\begin{array}{l}3<\frac{3}{\mathrm{two}}\left(0\right)+\mathrm{iii}\\ 3<0+3\\ 3<3\text{✗}\end{array}$	$\begin{array}{l}\mathrm{iii}\le \frac{\mathrm{iii}}{\mathrm{ii}}\left(0\right)+3\\ 3\le 0+3\\ 3\le \mathrm{iii}\text{✓}\end{array}$

And then far we have seen examples of inequalities that were "less than." Now consider the following graphs with the same purlieus:

Greater Than (Higher up)	Less Than (Below)
$y\ge \frac{\mathrm{three}}{2}x+3$	$y\le \frac{3}{2}x+\mathrm{iii}$

Given the graphs above, what might nosotros await if we use the origin (0, 0) as a test signal?

$y\ge \frac{3}{2}\mathrm{10}+3$	$y\le \frac{3}{\mathrm{ii}}x+3$
$\begin{array}{l}0\ge \frac{3}{2}\left(0\right)+3\\ 0\ge 0+3\\ 0\ge \mathrm{iii}\text{✗}\end{array}$	$\begin{array}{l}0\le \frac{3}{\mathrm{ii}}\left(0\right)+3\\ 0\le 0+3\\ 0\le 3\text{✓}\end{array}$

Example 1

Determine whether or not $\left(\mathrm{two},\frac{\mathrm{one}}{\mathrm{two}}\right)$ is a solution to $5\mathrm{10}-\mathrm{ii}y<\mathrm{ten}.$

Solution:

Substitute the x- and y-values into the equation and meet if a truthful statement is obtained.

$$\begin{array}{ccc}\hfill 5x-\mathrm{ii}y& <& \mathrm{x}\hfill \\ \hfill 5\left(\mathrm{two}\right)-\mathrm{ii}\left(\frac{1}{2}\right)& <& 10\hfill \\ \hfill \mathrm{ten}-1& <& 10\hfill \\ \hfill 9& <& 10\text{✓}\hfill \end{array}$$

Respond: $\left(\mathrm{two},\frac{1}{2}\right)$ is a solution.

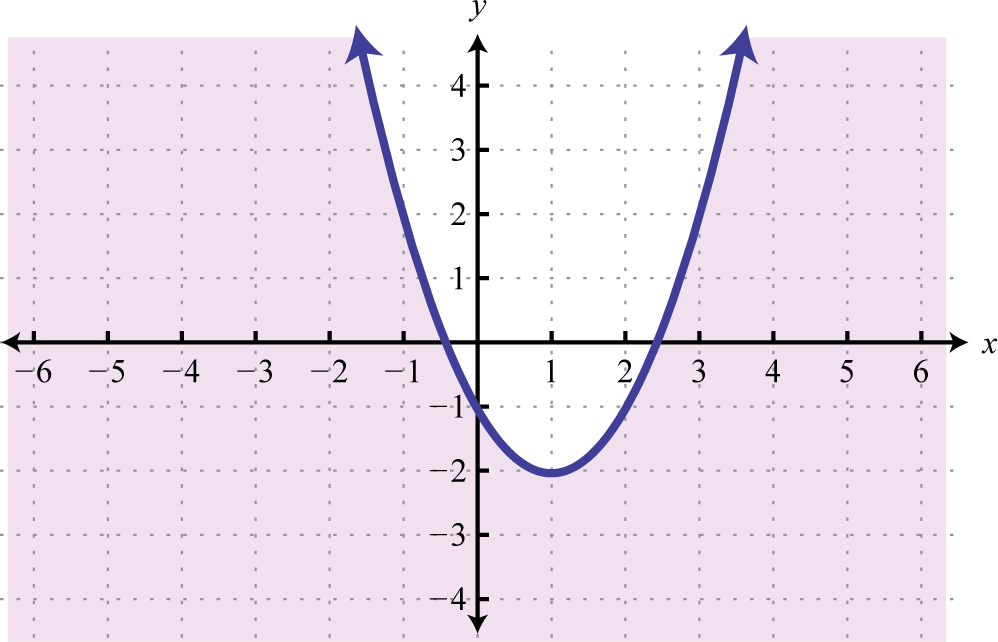
These ideas and techniques extend to nonlinear inequalities with 2 variables. For example, all of the solutions to $y>x^2$ are shaded in the graph below.

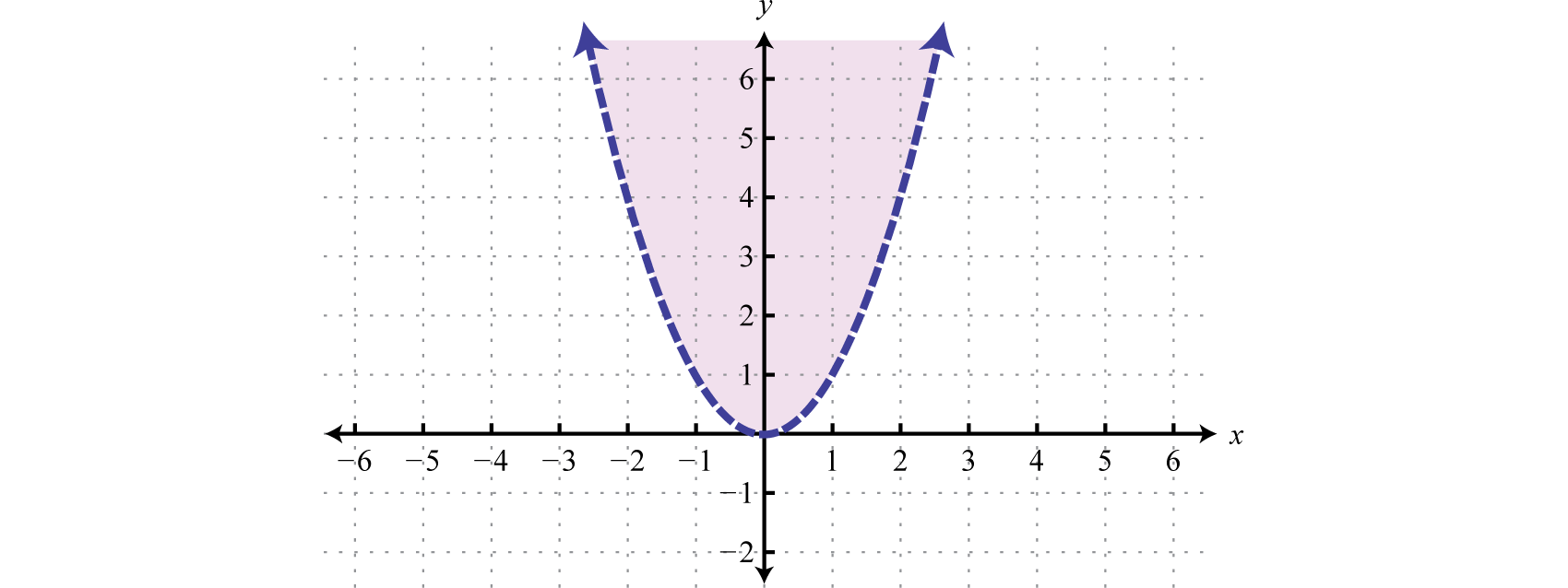
The boundary of the region is a parabola, shown as a dashed curve on the graph, and is non part of the solution set. Still, from the graph nosotros expect the ordered pair (−one,iv) to be a solution. Furthermore, we expect that ordered pairs that are not in the shaded region, such equally (−3, 2), will non satisfy the inequality.

Check (−1,4)	Check (−iii, two)
$\begin{array}{l}y>x^{\mathrm{two}}\\ 4>{\left(-1\right)}^{\mathrm{ii}}\\ \mathrm{iv}>\mathrm{i}\text{✓}\end{array}$	$\begin{array}{l}y>{\mathrm{10}}^2\\ \mathrm{two}>{\left(-3\right)}^{\mathrm{ii}}\\ 2>\mathrm{ix}\text{✗}\end{array}$

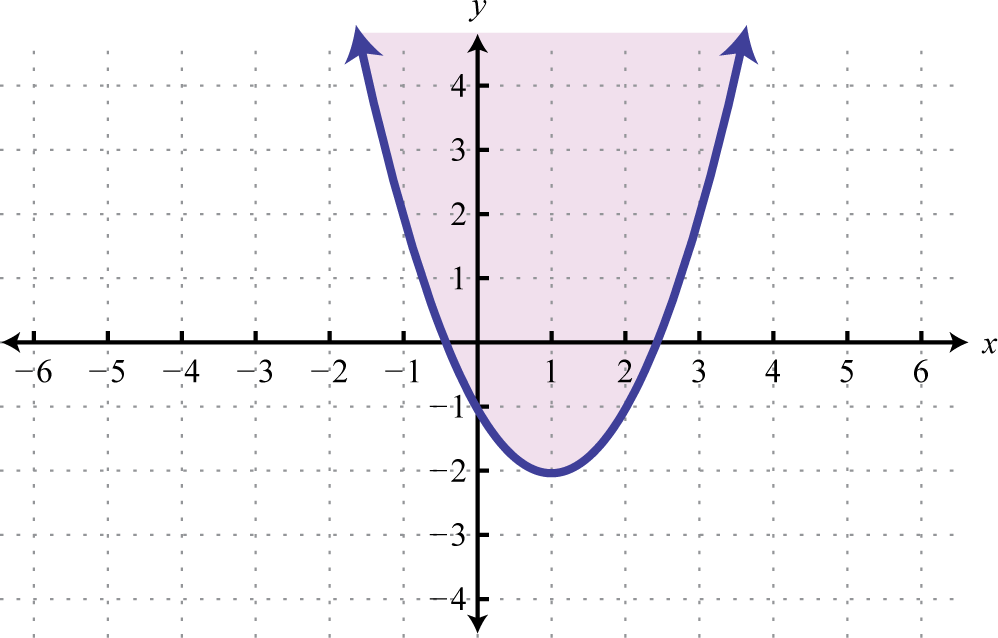
Following are graphs of solutions sets of inequalities with inclusive parabolic boundaries.

$y\le {\left(\mathrm{10}-1\right)}^2-2$	$y\ge {\left(x-1\right)}^2-\mathrm{two}$

You are encouraged to test points in and out of each solution ready that is graphed above.

Try this! Is $\left(-\mathrm{three},-2\right)$ a solution to $2\mathrm{10}-3y<0$ ?

Respond: No

Graphing Solutions to Inequalities with 2 Variables

Solutions to linear inequalities are a shaded half-plane, divisional by a solid line or a dashed line. This purlieus is either included in the solution or non, depending on the given inequality. If we are given a strict inequality, we use a dashed line to indicate that the boundary is not included. If nosotros are given an inclusive inequality, nosotros apply a solid line to indicate that it is included. The steps for graphing the solution set for an inequality with two variables are shown in the following example.

Instance 2

Graph the solution set $y>-3\mathrm{10}+\mathrm{i}.$

Solution:

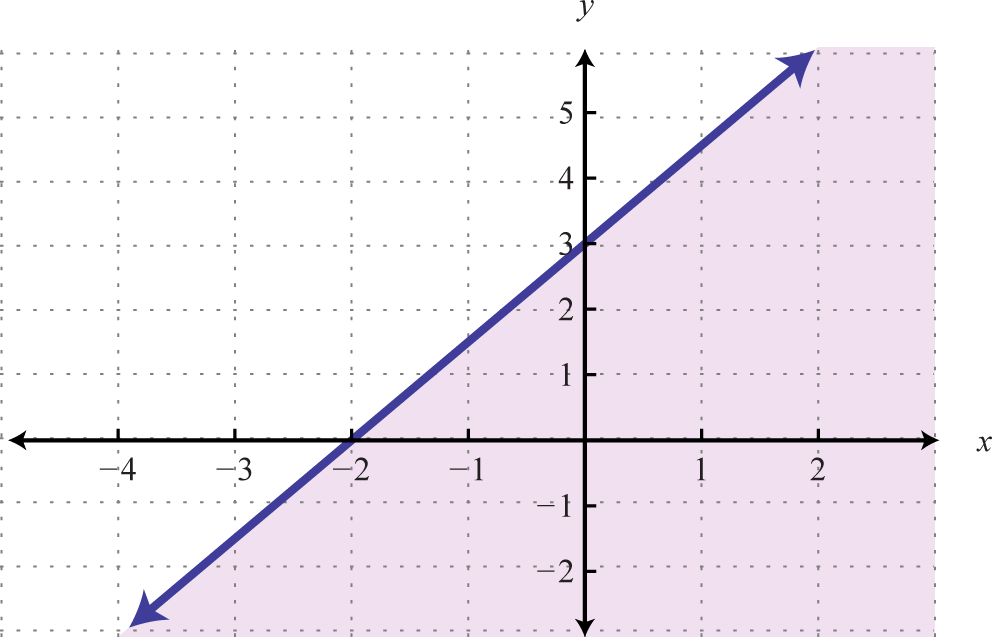
• Step 1: Graph the boundary. Because of the strict inequality, nosotros will graph the purlieus $y=-3x+\mathrm{one}$ using a dashed line. We tin can see that the slope is $k=-\mathrm{three}=\frac{-\mathrm{iii}}{1}=\frac{rise}{run}$ and the y-intercept is (0, 1).

  

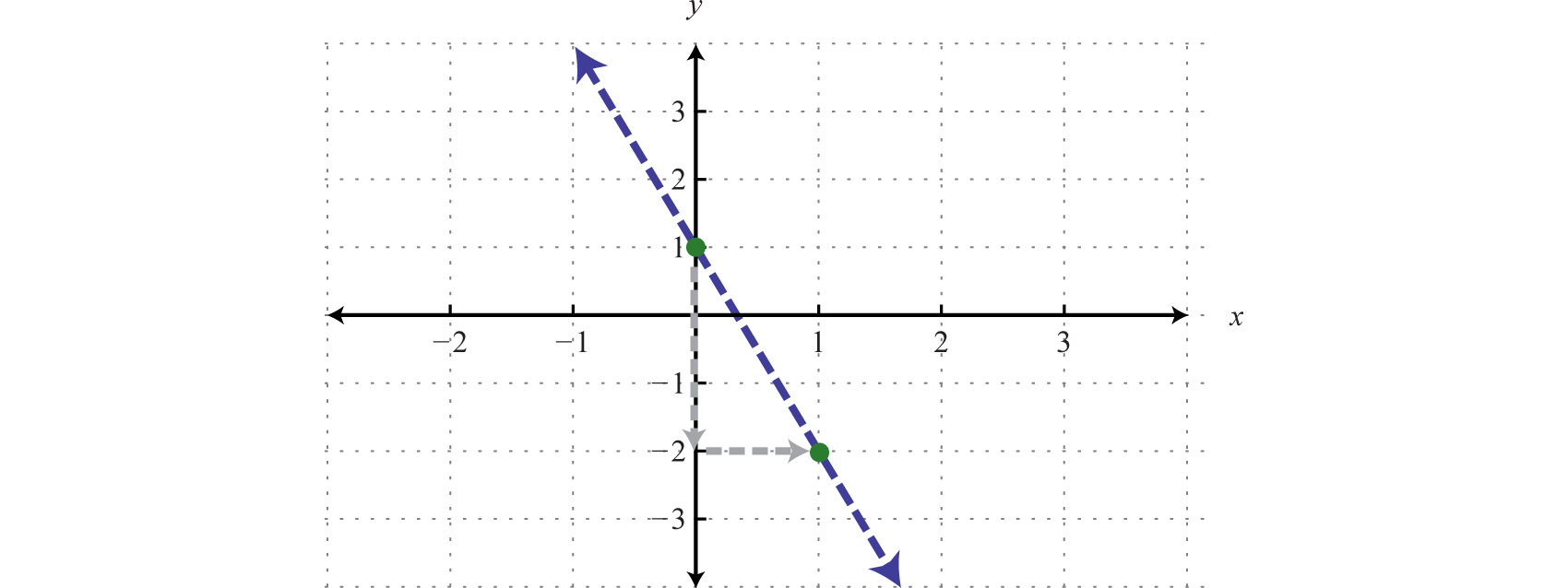
• Step ii: Test a point that is not on the purlieus. A common test signal is the origin, (0, 0). The examination signal helps us determine which half of the aeroplane to shade.

  Test point	$y>-3x+1$
  (0, 0)	$\begin{array}{l}0>-3(0)+\mathrm{one}\\ 0>1\text{✗}\end{array}$

• Step iii: Shade the region containing the solutions. Since the test point (0, 0) was not a solution, it does non lie in the region containing all the ordered pair solutions. Therefore, shade the half of the airplane that does not contain this test point. In this example, shade above the purlieus line.

Answer:

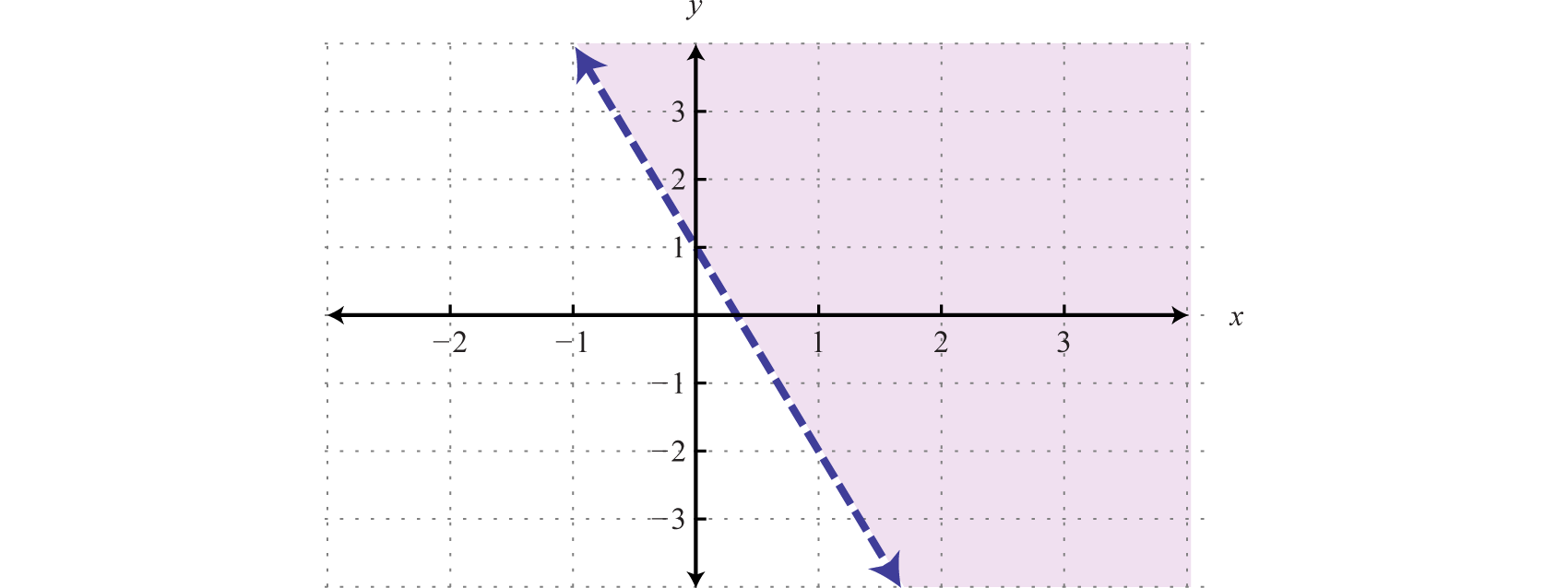
Consider the trouble of shading to a higher place or below the boundary line when the inequality is in slope-intercept form. If $y>gx+b$ , then shade above the line. If $y<\mathrm{1000}x+b$ , and so shade below the line. Shade with circumspection; sometimes the purlieus is given in standard form, in which case these rules do not apply.

Instance three

Graph the solution gear up $\mathrm{ii}x-5y\ge -\mathrm{x}.$

Solution:

Here the purlieus is divers by the line $\mathrm{two}x-5y=-\mathrm{x}.$ Since the inequality is inclusive, we graph the boundary using a solid line. In this case, graph the boundary line using intercepts.

To find the 10-intercept, fix y = 0.	To find the y-intercept, set ten = 0.
$2\mathrm{ten}-\mathrm{five}y=-\mathrm{ten}$ $\begin{array}{ccc}\hfill 2x-5\left(0\right)& =& -10\hfill \\ \hfill 2x& =& -\mathrm{ten}\hfill \\ \hfill \mathrm{ten}& =& -5\hfill \end{array}$	$2x-\mathrm{v}y=-10$ $\begin{array}{ccc}\hfill 2\left(0\right)-\mathrm{five}y& =& -10\hfill \\ \hfill -5y& =& -\mathrm{ten}\hfill \\ \hfill y& =& \mathrm{ii}\hfill \end{array}$
x-intercept: (−5, 0)	y-intercept: (0, two)

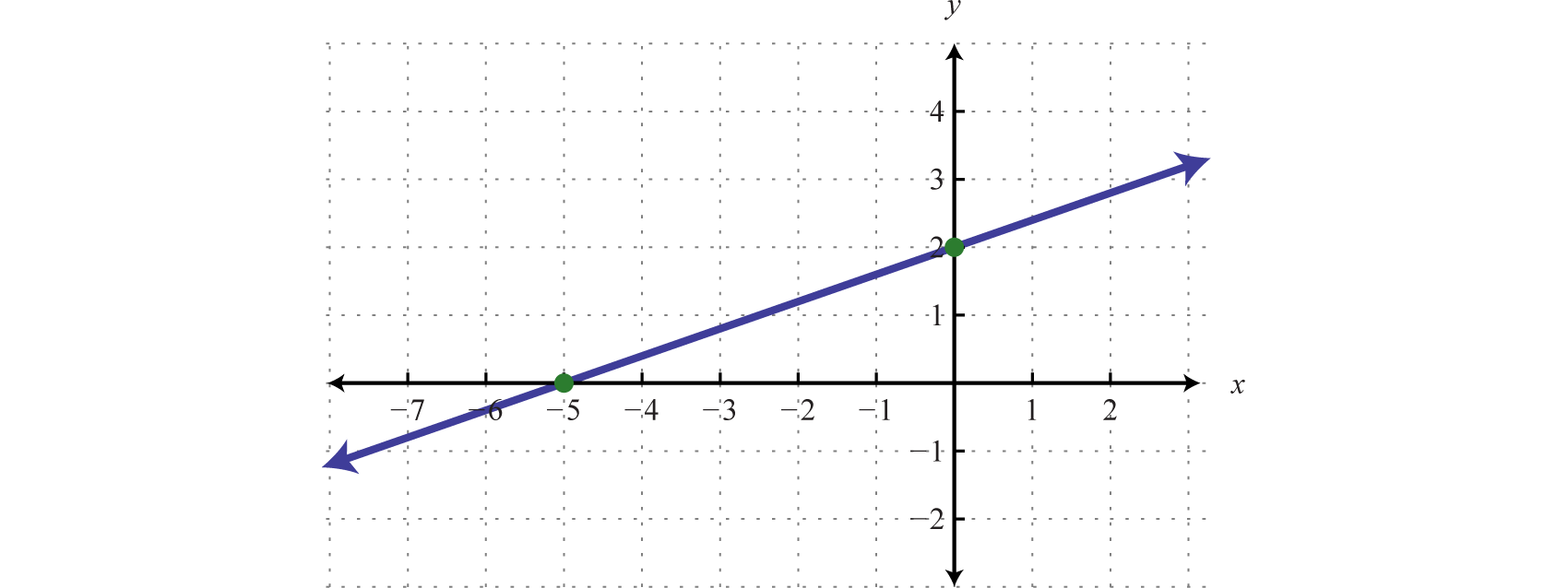
Next, test a point; this helps decide which region to shade.

Test indicate	$2\mathrm{ten}-5y\ge -10$
(0, 0)	$\begin{array}{ccc}\hfill 2\left(0\right)-5\left(0\right)& \ge & -10\hfill \\ \hfill 0& \ge & -\mathrm{ten}\text{✓}\hfill \end{array}$

Since the exam point is in the solution set, shade the half of the airplane that contains it.

Answer:

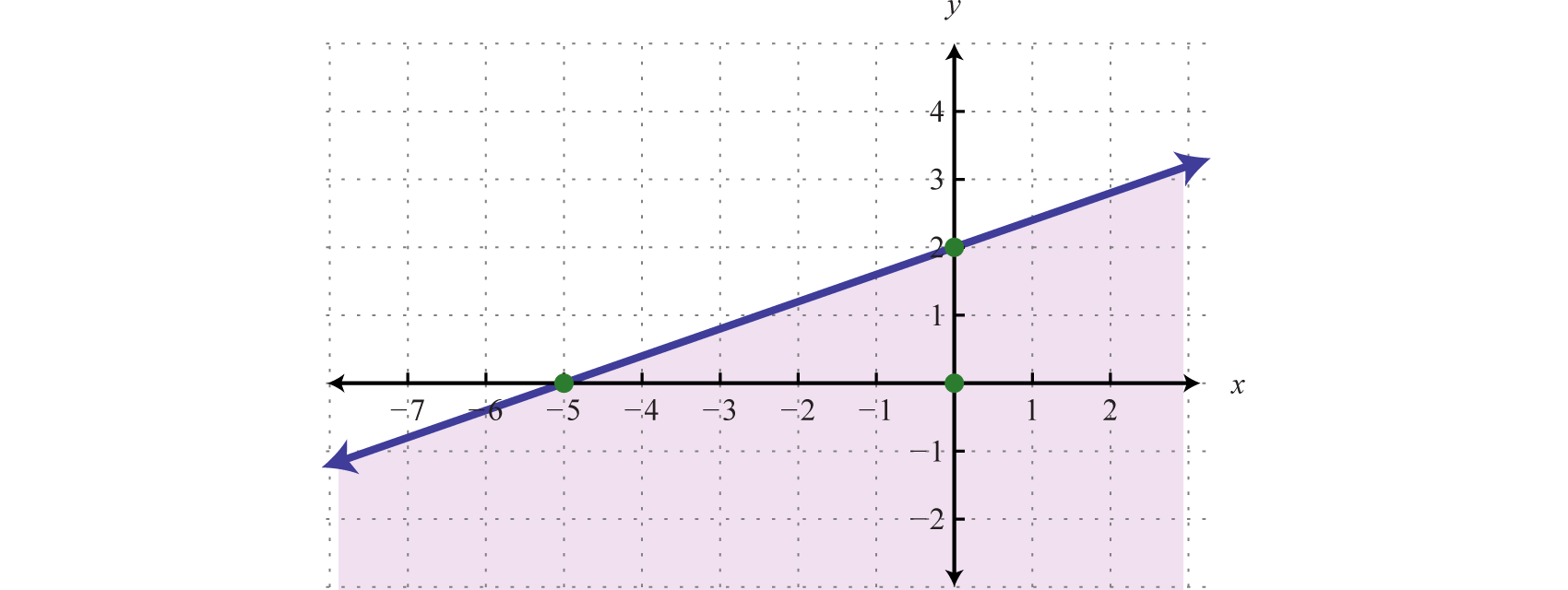
In this case, detect that the solution ready consists of all the ordered pairs below the boundary line. This may seem counterintuitive considering the original inequality involved "greater than" $\ge .$ This illustrates that it is a best exercise to actually test a betoken. Solve for y and you see that the shading is correct.

$$\begin{array}{ccc}\hfill \mathrm{two}x-5y& \ge & -10\hfill \\ \hfill 2x-5y-\mathrm{two}\mathrm{ten}& \ge & -10-2x\hfill \\ \hfill -\mathrm{v}y& \ge & -2\mathrm{10}-10\hfill \\ \hfill \frac{-5y}{-5}& \le & \frac{-2\mathrm{ten}-10}{-\mathrm{v}}R\mathrm{east}verseth\mathrm{east}inequality.\hfill \\ \hfill y& \le & \frac{\mathrm{ii}}{\mathrm{v}}x+2\hfill \end{array}$$

In gradient-intercept form, yous tin can come across that the region below the boundary line should exist shaded. An alternate approach is to first express the boundary in slope-intercept form, graph it, so shade the advisable region.

Example 4

Graph the solution set $y<\mathrm{ii}.$

Solution:

Get-go, graph the purlieus line $y=\mathrm{two}$ with a dashed line because of the strict inequality. Adjacent, test a indicate.

Test point	$y<2$
(0, 0)	$0<2\text{✓}$

In this example, shade the region that contains the exam point.

Answer:

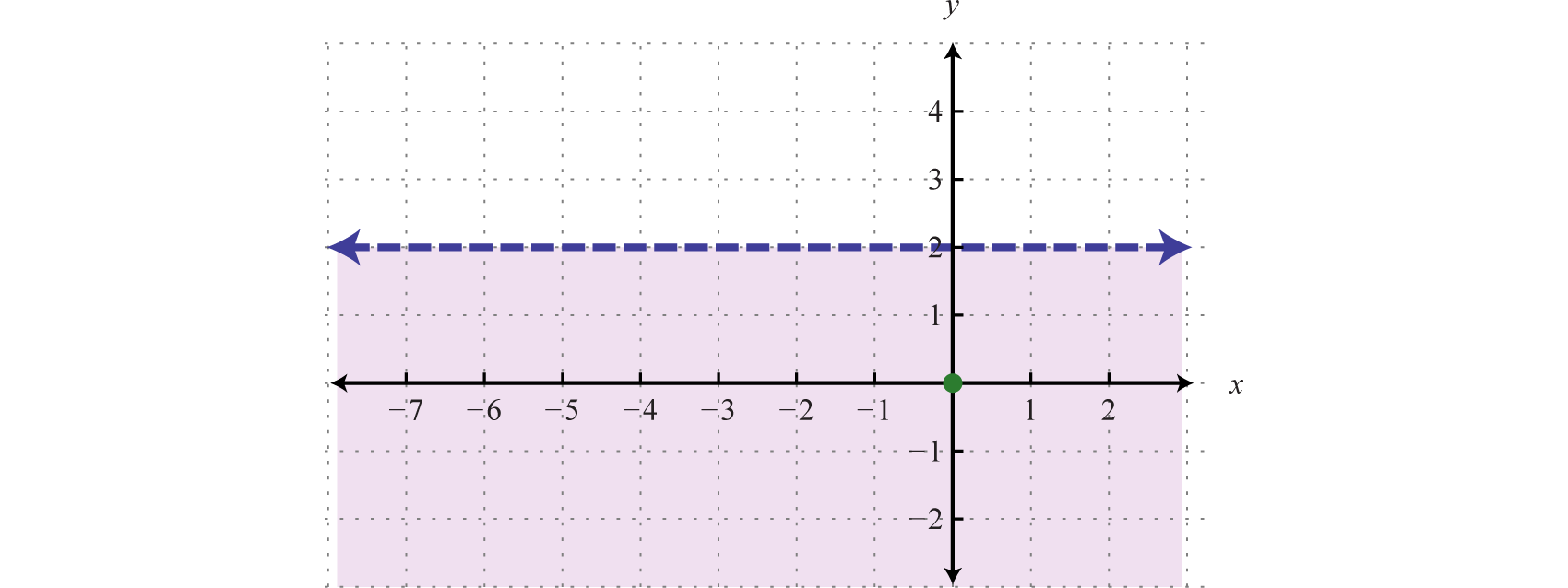
Attempt this! Graph the solution prepare $\mathrm{ii}x-\mathrm{iii}y<0.$

Answer:

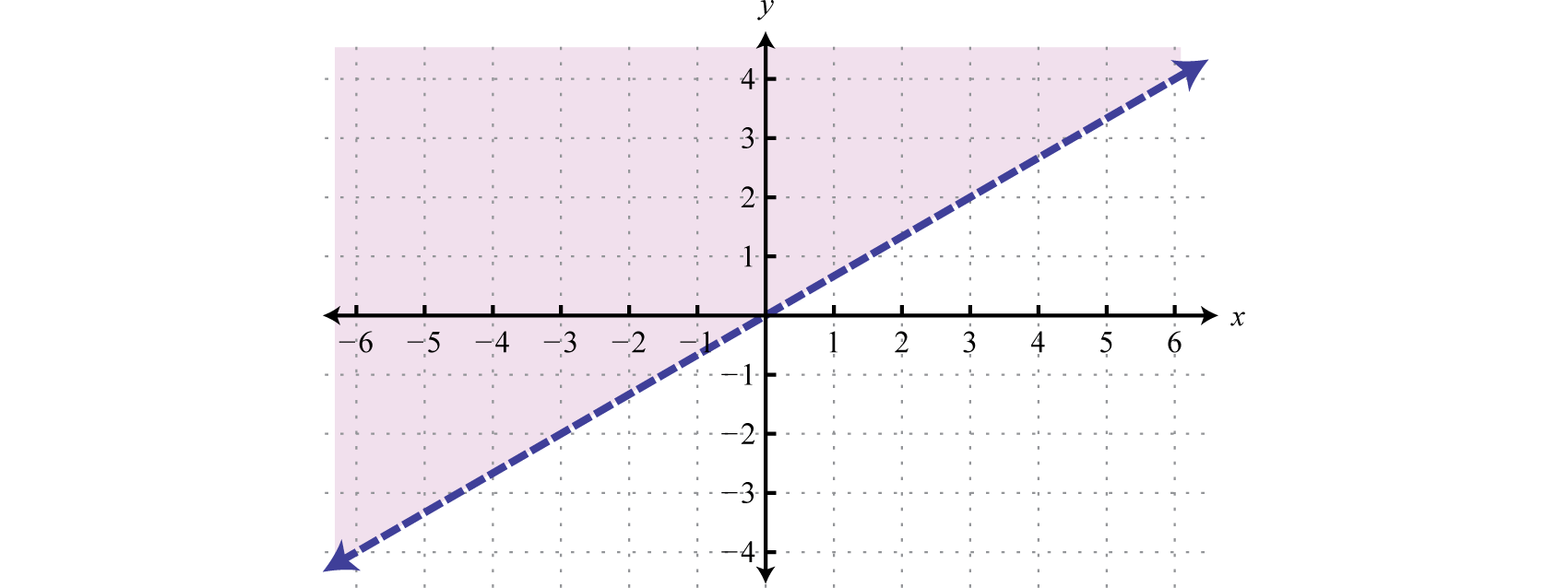
The steps are the same for nonlinear inequalities with ii variables. Graph the boundary first and then examination a indicate to make up one's mind which region contains the solutions.

Case 5

Graph the solution set $y<{\left(x+2\right)}^2-\mathrm{ane}.$

Solution:

The boundary is a bones parabola shifted 2 units to the left and one unit of measurement down. Brainstorm by cartoon a dashed parabolic purlieus considering of the strict inequality.

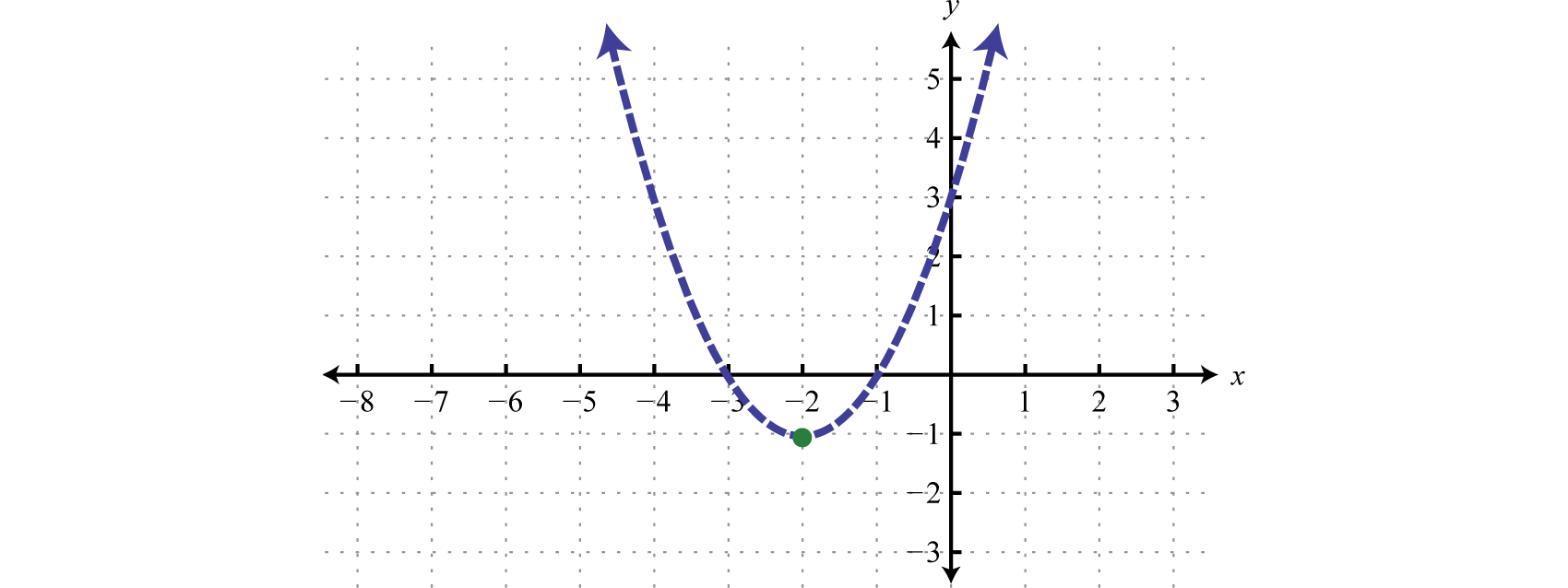
Next, test a indicate.

Examination point	$y<{\left(\mathrm{10}+2\right)}^2-1$
(0, 0)	$\begin{array}{l}0<{\left(0+\mathrm{two}\right)}^2-1\\ 0<4-1\\ 0<3\text{✓}\end{array}$

In this case, shade the region that contains the test point $\left(0,0\right).$

Answer:

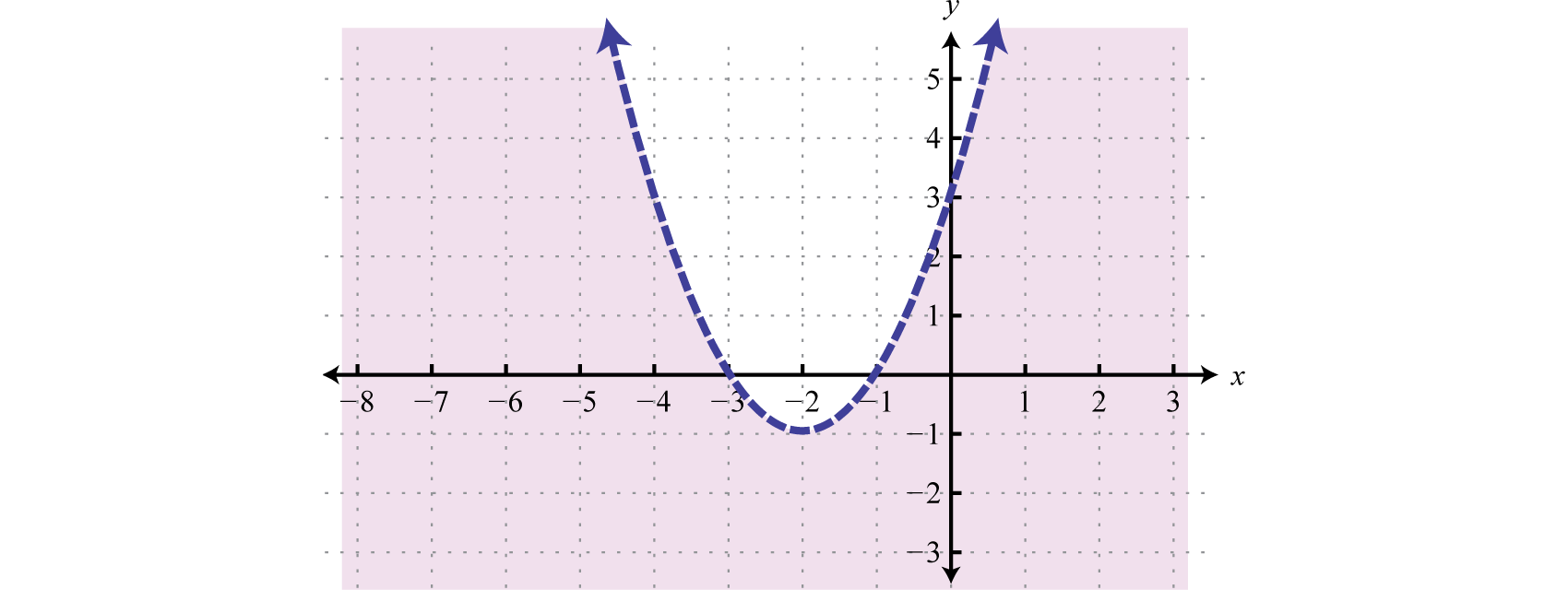
Example six

Graph the solution gear up $y\ge {\mathrm{ten}}^2+3.$

Solution:

The boundary is a basic parabola shifted 3 units upwardly. Information technology is graphed using a solid curve because of the inclusive inequality.

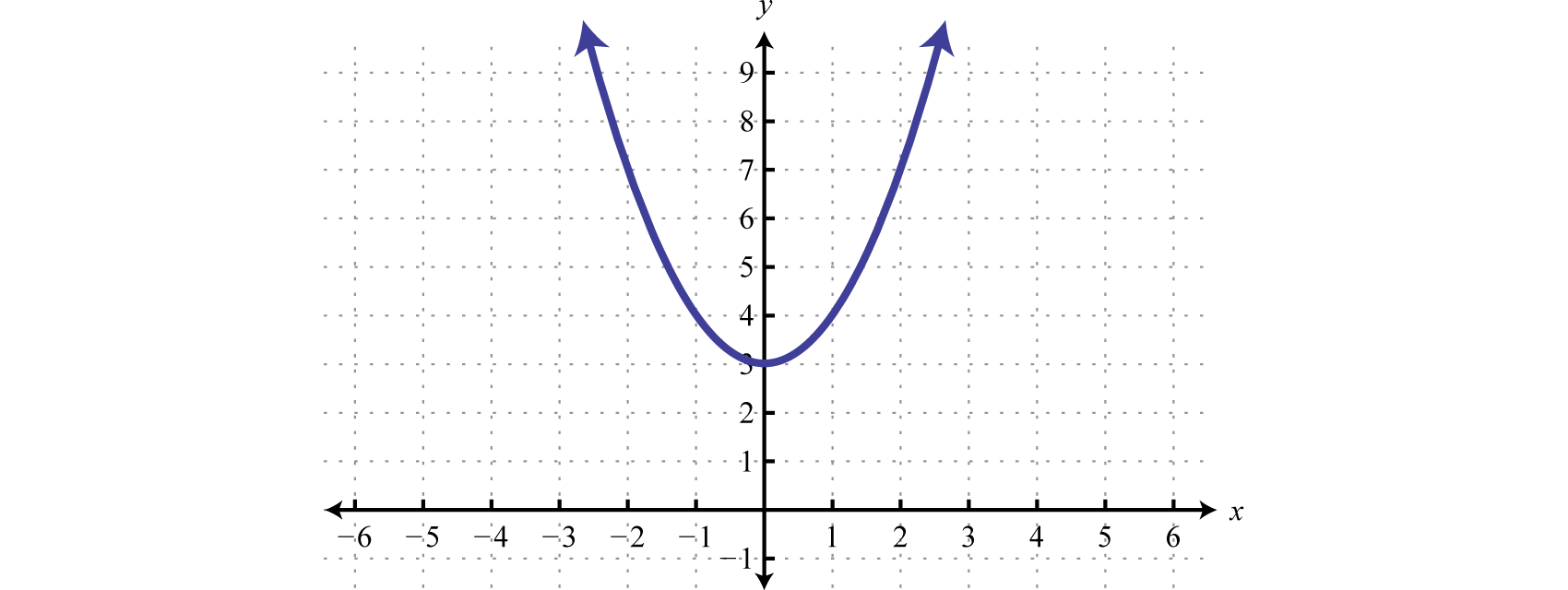
Next, test a signal.

Test point	$y\ge {\mathrm{10}}^2+3$
(0, 0)	$\begin{array}{l}0\ge 0^{\mathrm{ii}}+\mathrm{three}\\ 0\ge 3\text{✗}\end{array}$

In this case, shade the region that does non contain the test point $\left(0,0\right).$

Reply:

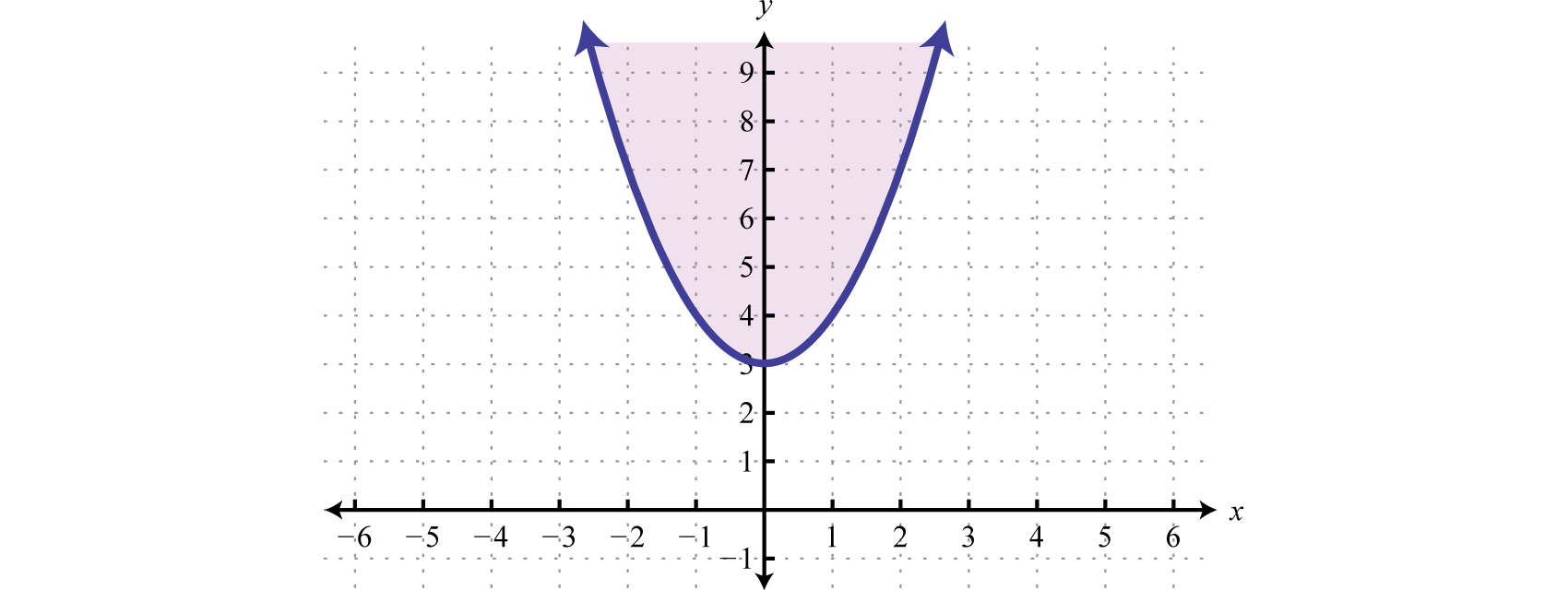
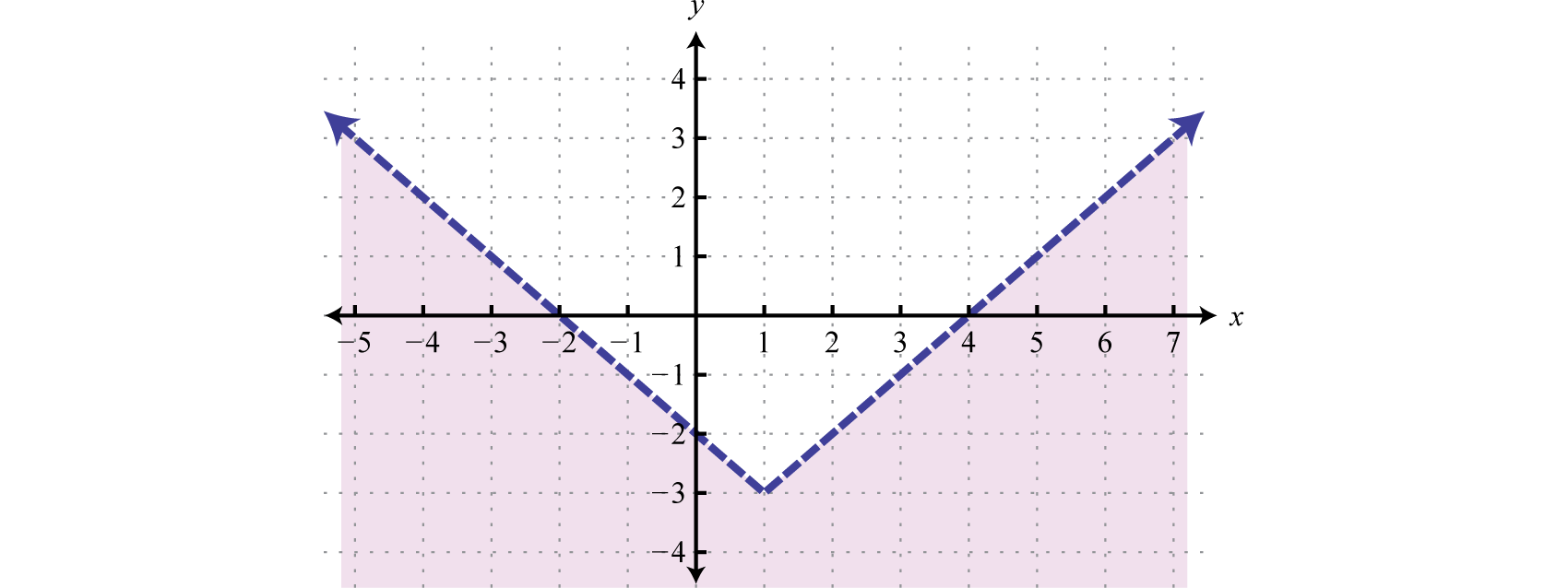
Try this! Graph the solution gear up $y<\left|x-1\right|-3.$

Answer:

Cardinal Takeaways

• Linear inequalities with two variables have infinitely many ordered pair solutions, which can be graphed by shading in the appropriate half of a rectangular coordinate airplane.
• To graph the solution prepare of an inequality with 2 variables, first graph the boundary with a dashed or solid line depending on the inequality. If given a strict inequality, use a dashed line for the purlieus. If given an inclusive inequality, use a solid line. Next, choose a test signal not on the purlieus. If the examination point solves the inequality, then shade the region that contains it; otherwise, shade the opposite side.
• Check your answer by testing points in and out of the shading region to verify that they solve the inequality or not.

Topic Exercises

Part A: Solutions to Inequalities with Ii Variables

Is the ordered pair a solution to the given inequality?

1. $5x-y>-\mathrm{two}\text{;}\left(-3,-\mathrm{four}\right)$

2. $\mathrm{iv}x-y<-8\text{;}\left(-3,-10\right)$

3. $$\mathrm{half\; dozen}x-\mathrm{xv}y\ge -1\text{;}\left(\frac{1}{2},-\frac{\mathrm{i}}{3}\right)$$

4. $$\mathrm{ten}-2y\ge 2\text{;}\left(\frac{2}{\mathrm{iii}},-\frac{5}{\mathrm{half-dozen}}\right)$$

5. $$\frac{3}{\mathrm{iv}}\mathrm{10}-\frac{\mathrm{two}}{3}y<\frac{3}{2}\text{;}\left(\mathrm{i},-1\right)$$

6. $$\frac{2}{5}\mathrm{10}+\frac{\mathrm{four}}{3}y>\frac{1}{\mathrm{two}}\text{;}\left(-\mathrm{ii},\mathrm{ane}\right)$$

7. $y\le x^2-1$ ; $\left(-\mathrm{ane},\mathrm{ane}\right)$

8. $y\ge x^2+3$ ; $\left(-\mathrm{ii},0\right)$

9. $y\ge {\left(\mathrm{ten}-5\right)}^{\mathrm{two}}+\mathrm{one}$ ; $\left(3,4\right)$

10. $y\le 2{\left(x+1\right)}^2-3$ ; $\left(-1,-2\right)$

11. $y>3-\left|x\right|$ ; $\left(-4,-3\right)$

12. $y<\left|x\right|-\mathrm{viii}$ ; $\left(5,-\mathrm{seven}\right)$

13. $y>\left|2x-\mathrm{ane}\right|-\mathrm{iii}$ ; $\left(-1,3\right)$

14. $y<\left|3x-\mathrm{two}\right|+\mathrm{two}$ ; $\left(-2,10\right)$

Part B: Graphing Solutions to Inequalities with Two Variables.

Graph the solution prepare.

15. $y<\mathrm{two}\mathrm{ten}-\mathrm{one}$

16. $y>-4x+\mathrm{ane}$

17. $y\ge -\frac{2}{3}\mathrm{ten}+3$

18. $y\le \frac{4}{3}x-3$

19. $2x+\mathrm{three}y\le 18$

20. $\mathrm{five}x+2y\le 8$

21. $6x-5y>30$

22. $8x-\mathrm{vi}y<24$

23. $3x-4y<0$

24. $\mathrm{ten}-3y>0$

25. $x+y\ge 0$

26. $x-y\ge 0$

27. $y\le -2$

28. $y>-\mathrm{iii}$

29. $x<-2$

30. $x\ge -\mathrm{three}$

31. $$\frac{1}{\mathrm{half\; dozen}}x+\frac{1}{\mathrm{ten}}y\le \frac{\mathrm{i}}{2}$$

32. $$\frac{3}{\mathrm{viii}}x+\frac{\mathrm{one}}{2}y\ge \frac{3}{\mathrm{iv}}$$

33. $$\frac{1}{12}x-\frac{\mathrm{ane}}{6}y<\frac{2}{3}$$

34. $$\frac{1}{\mathrm{iii}}\mathrm{10}-\frac{1}{9}y>\frac{\mathrm{iv}}{\mathrm{three}}$$

35. $5x\le -4y-12$

36. $-4x\le 12-\mathrm{three}y$

37. $\mathrm{iv}y+\mathrm{ii}<3\mathrm{ten}$

38. $8x<\mathrm{nine}-6y$

39. $\mathrm{five}\ge 3x-15y$

40. $$2\mathrm{ten}\ge 6-\mathrm{ix}y$$

41. Write an inequality that describes all points in the upper half-plane to a higher place the x-axis.

42. Write an inequality that describes all points in the lower half-airplane below the x-centrality.

43. Write an inequality that describes all points in the one-half-aeroplane left of the y-axis.

44. Write an inequality that describes all points in the half-plane right of the y-axis.

45. Write an inequality that describes all ordered pairs whose y-coordinate is at least grand units.

46. Write an inequality that describes all ordered pairs whose x-coordinate is at well-nigh yard units.

Graph the solution fix.

47. $y\le {\mathrm{ten}}^2+\mathrm{iii}$

48. $y>x^2-\mathrm{ii}$

49. $y\le -{\mathrm{ten}}^2$

50. $y\ge -{\mathrm{10}}^2$

51. $y>{\left(\mathrm{ten}+\mathrm{one}\right)}^{\mathrm{two}}$

52. $y>{\left(x-\mathrm{ii}\right)}^2$

53. $y\le {\left(x-\mathrm{ane}\right)}^2+2$

54. $y\le {\left(x+\mathrm{iii}\right)}^{\mathrm{two}}-1$

55. $y<-x^2+1$

56. $y>-{\left(x-2\right)}^2+1$

57. $y\ge \left|x\right|-\mathrm{ii}$

58. $y<\left|x\right|+1$

59. $y<\left|x-3\right|$

60. $y\le \left|\mathrm{10}+\mathrm{two}\right|$

61. $y>-\left|\mathrm{ten}+1\right|$

62. $y\le -\left|\mathrm{10}-\mathrm{ii}\right|$

63. $y\ge \left|\mathrm{10}+\mathrm{three}\right|-2$

64. $y\ge \left|x-2\right|-1$

65. $y<-\left|x+4\right|+2$

66. $y>-\left|x-\mathrm{iv}\right|-1$

67. $y>{\mathrm{ten}}^3-1$

68. $y\le {\mathrm{10}}^3+2$

69. $y\le \sqrt{x}$

70. $y>\sqrt{x}-\mathrm{i}$

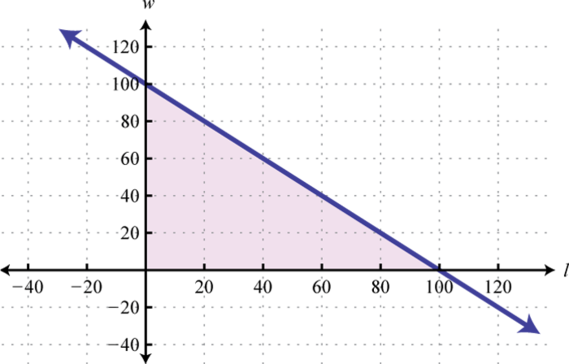
71. A rectangular pen is to be synthetic with at most 200 feet of fencing. Write a linear inequality in terms of the length fifty and the width westward. Sketch the graph of all possible solutions to this problem.

72. A visitor sells 1 production for $eight and another for $12. How many of each product must be sold so that revenues are at least $2,400? Let x stand for the number of products sold at $8 and let y correspond the number of products sold at $12. Write a linear inequality in terms of x and y and sketch the graph of all possible solutions.

Answers

1. No

3. Yes

5. Yes

7. No

9. No

11. No

13. Yes

15. 

17. 

19. 

21. 

23. 

25. 

27. 

29. 

31. 

33. 

35. 

37. 

39. 

41. $y>0$

43. $x<0$

45. $y\ge k$

47. 

49. 

51. 

53. 

55. 

57. 

59. 

61. 

63. 

65. 

67. 

69. 

71. $l+w\le 100$ ;

    

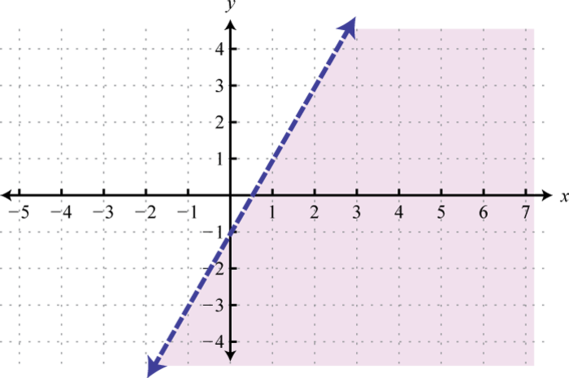
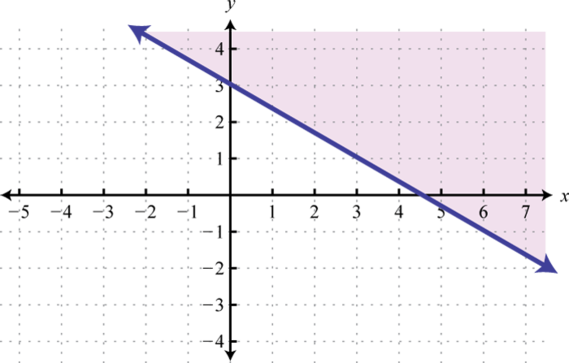
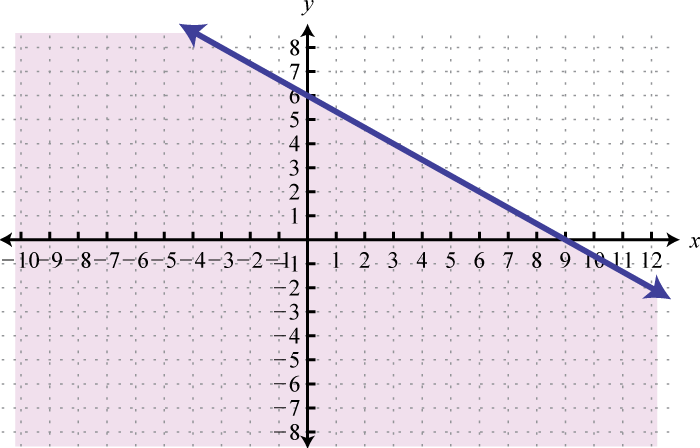
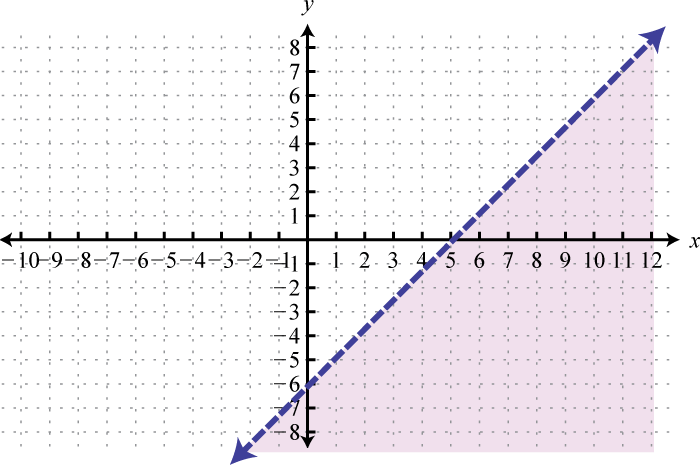
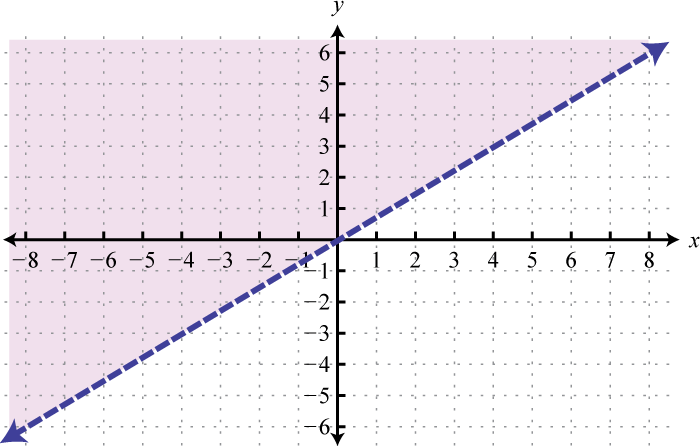
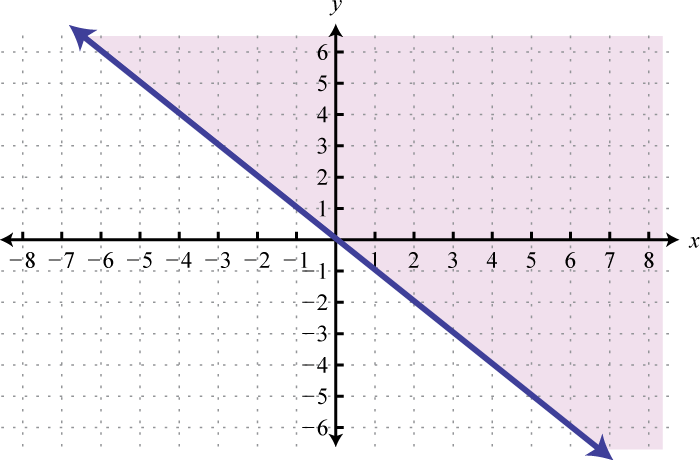
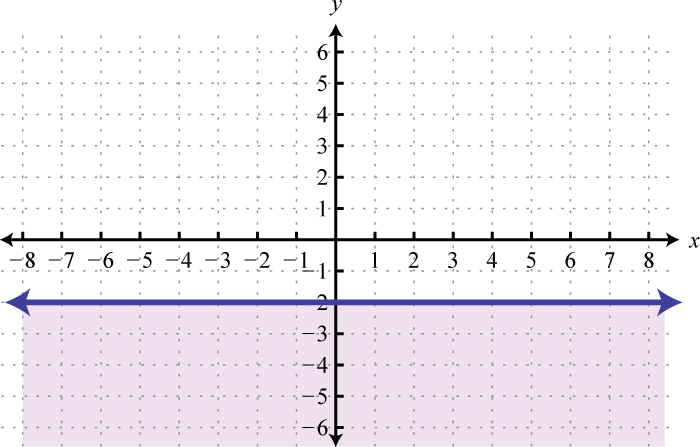
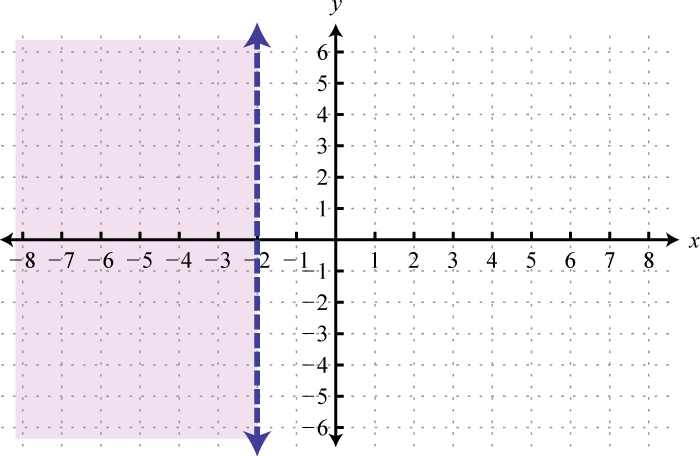
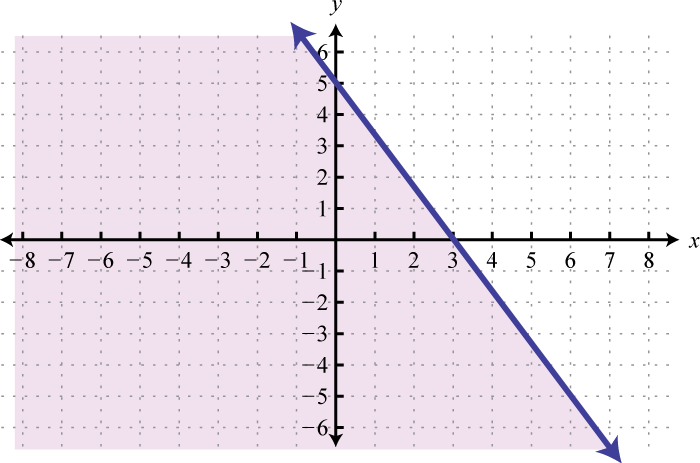
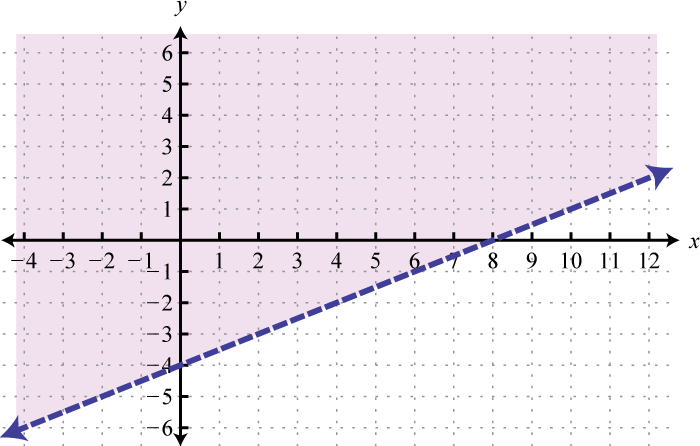
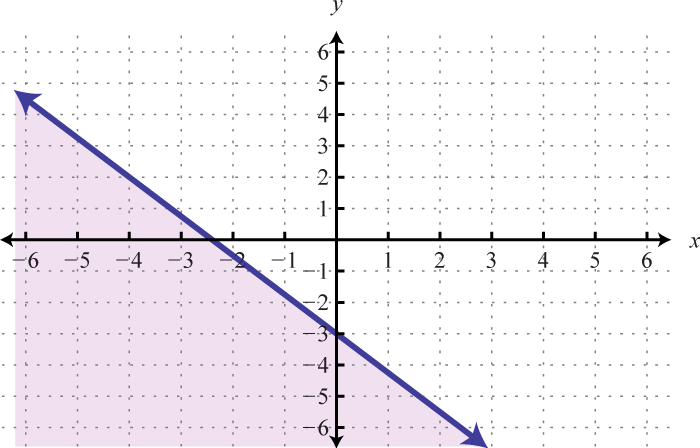
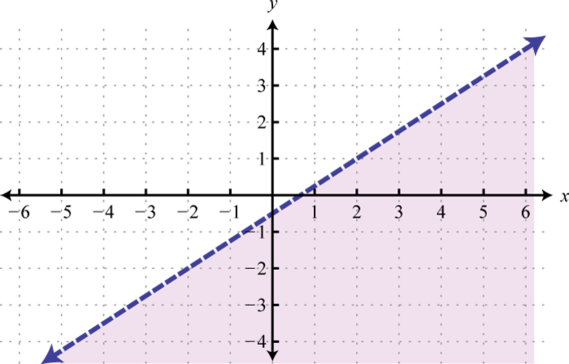
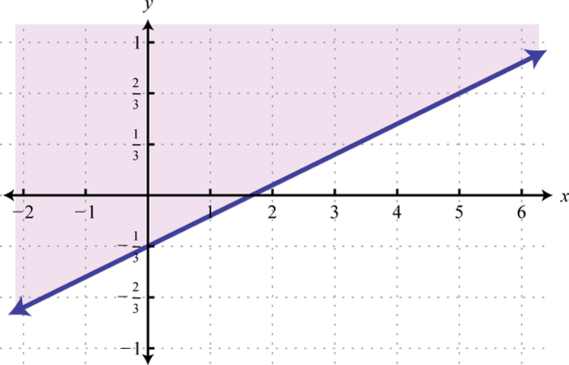
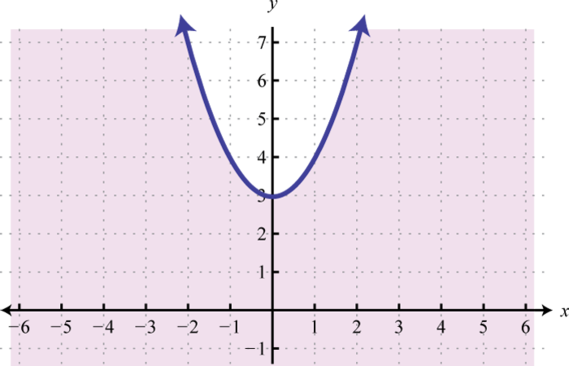
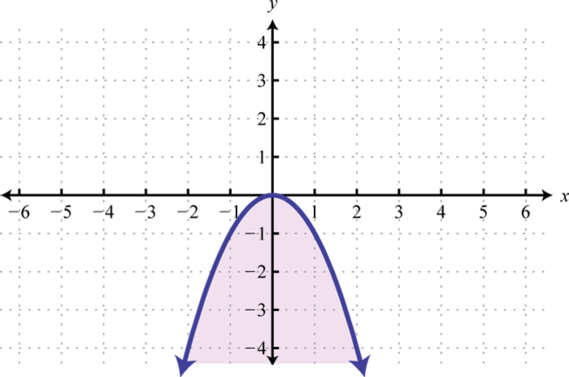
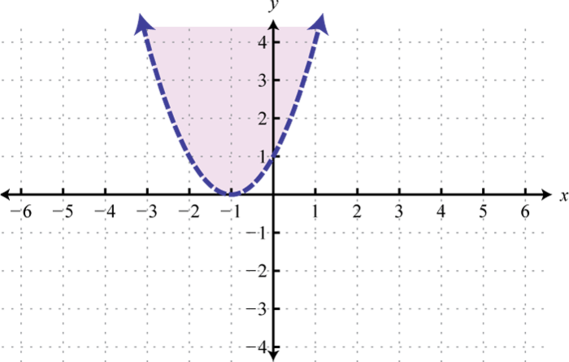
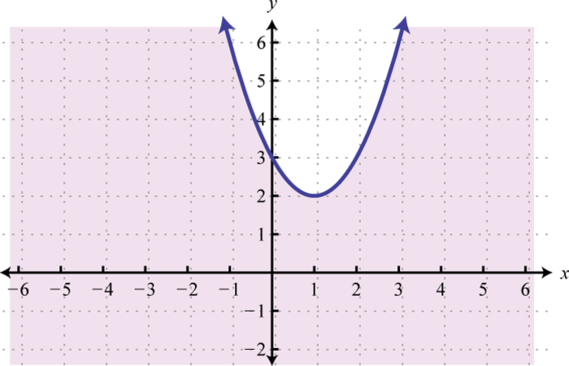
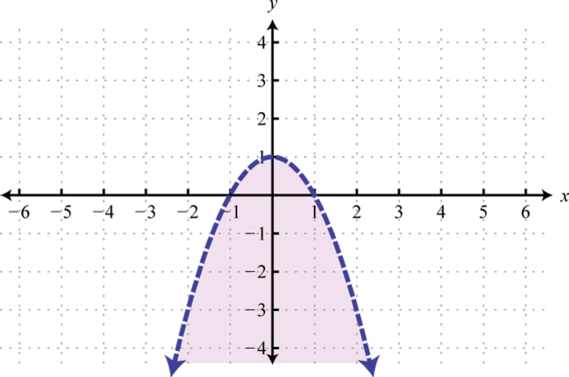
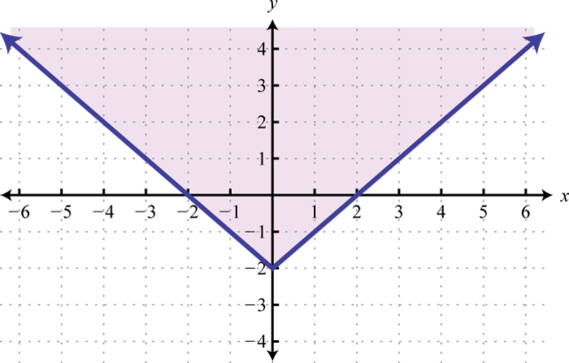
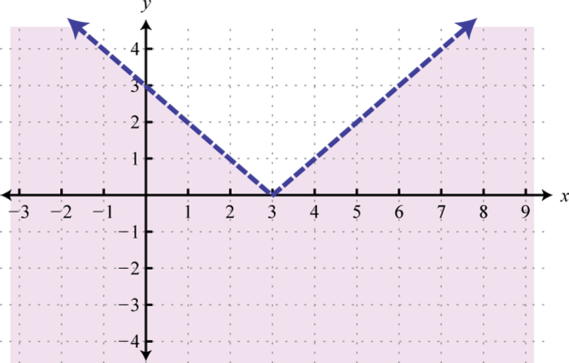
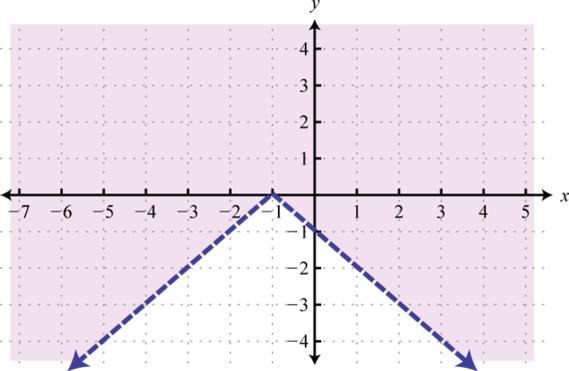
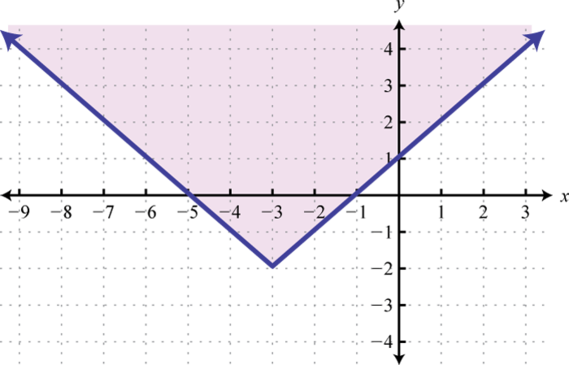
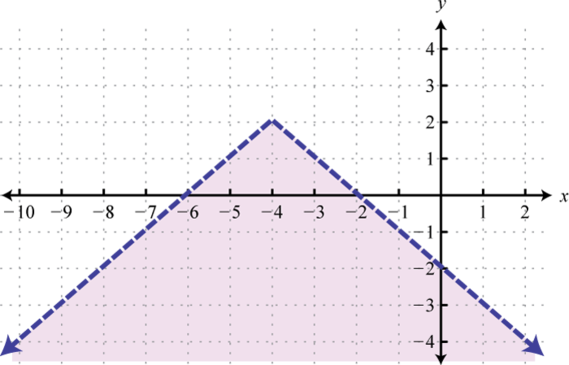
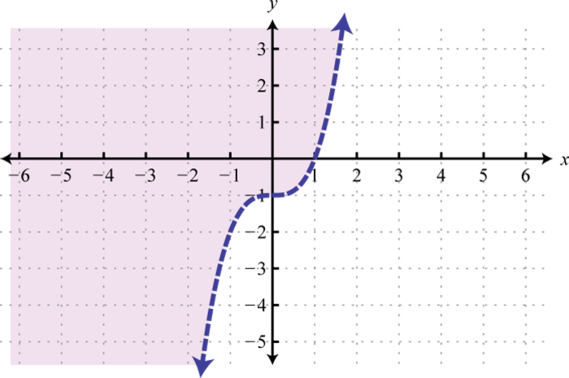
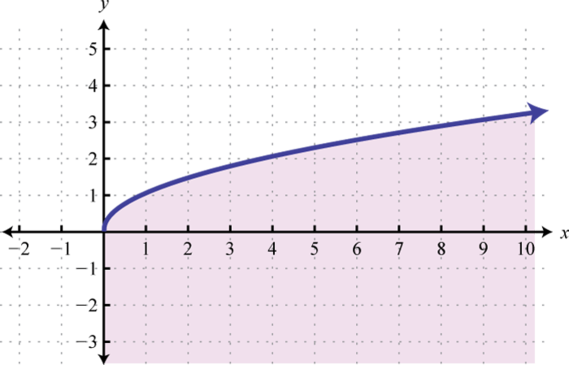
Source: https://saylordotorg.github.io/text_intermediate-algebra/s05-07-solving-inequalities-with-two-.html

Share this post